What Are Epicyclic Gears Used for?
Epicyclic gears also known as planetary gear systems, are widely utilized across various industries due to their compact design, high efficiency, and versatilit

These gears are primarily used in applications where space is limited, but high torque and speed variability are essential.
1. Automotive Transmissions: Epicyclic gears are a key component in automatic transmissions, providing seamless gear changes, high torque at low speeds, and efficient power transfer.
2. Industrial Machinery: They are used in heavy machinery for their ability to handle high loads, distribute torque evenly, and operate efficiently in compact spaces.
3. Aerospace: These gears play a crucial role in aircraft engines and helicopter rotors, ensuring reliability and precise motion control under demanding conditions.
4. Robotics and Automation: In robotics, epicyclic gears are used to achieve precise motion control, compact design, and high torque in limited spaces.
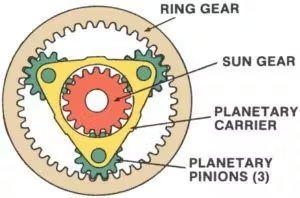
What Are the Four Elements of the Epicyclic Gear Set?
An epicyclic gear set, also known as a planetary gear system, is a highly efficient and compact mechanism commonly used in automotive transmissions, robotics, and industrial machinery. This system is composed of four key elements:
1.Sun Gear: Positioned at the center of the gear set, the sun gear is the primary driver or receiver of motion. It engages directly with the planet gears and often serves as the input or output of the system.
2. Planet Gears: These are multiple gears that rotate around the sun gear. Mounted on a planet carrier, they mesh with both the sun gear and the ring gear. The planet gears distribute the load evenly, making the system capable of handling high torque.
3.Planet Carrier: This component holds the planet gears in place and supports their rotation around the sun gear. The planet carrier can act as an input, output, or stationary element depending on the system’s configuration.
4.Ring Gear: This is a large outer gear that encircles the planet gears. The inner teeth of the ring gear mesh with the planet gears. Like the other elements, the ring gear can serve as an input, output, or remain stationary.
The interplay of these four elements provides the flexibility to achieve different speed ratios and directional changes within a compact structure.
How to Calculate Gear Ratio in an Epicyclic Gear Set?
The gear ratio of an epicyclic gear set depends on which components are fixed, input, and output. Here’s a step-by-step guide to calculating the gear ratio:
1.Understand the System Configuration:
Identify which element (sun, planet carrier, or ring) is stationary.
Determine the input and output components.
2. Use the Fundamental Gear Ratio Equation: The gear ratio of an epicyclic gear system can be calculated using:
GR = 1 + (R / S)
Where:
GR = Gear Ratio
R = Number of teeth on the ring gear
S = Number of teeth on the sun gear
This equation applies when the planet carrier is the output, and either the sun or the ring gear is stationary.
3.Adjust for Other Configurations:
- If the sun gear is stationary, the system’s output speed is influenced by the ratio of the ring gear and the planet carrier.
- If the ring gear is stationary, the output speed is determined by the relationship between the sun gear and the planet carrier.
4.Reverse Gear Ratio for Output to Input: When calculating speed reduction (input higher than output), the ratio is straightforward. For speed multiplication (output higher than input), invert the calculated ratio.

Example Calculation:
Suppose a gear set has:
Ring Gear (R): 72 teeth
Sun Gear (S): 24 teeth
If the planet carrier is the output and the sun gear is stationary, the gear ratio is:
GR = 1 + (72 / 24) GR = 1 + 3 = 4
This means the output speed will be 4 times slower than the input speed, providing a 4:1 reduction ratio.
Understanding these principles allows engineers to design efficient an versatile systems tailored to specific applications.
Post time: Dec-06-2024